Below are all the formulas and calculations we use to determine the significance of an experiment.
Bayesian experimentation
In the field of experimentation, there are two primary statistical approaches: frequentist and Bayesian.
We adopt the Bayesian methodology because it directly answers the question: "Is variant A better than variant B?". This approach minimizes judgment errors, which are more common with the frequentist method.
Our Bayesian experimentation method focuses on two key parameters during experiments:
- Probability of each variant being the best: This metric helps us understand which variant is more likely to outperform the other.
- Significance of the results: We evaluate whether the observed differences between variants are statistically meaningful.
Funnel experiment calculations
Funnel experiments compare conversion rates. For example, if you want to measure the change in the conversion rate for subscribing to your site, you would use this type of experiment.
1. Probability of being the best
We use Monte Carlo simulations to determine the probability of each variant being the best.
Each variant can be modeled as a beta distribution, with the alpha parameter equal to the number of conversions and the beta parameter equal to the number of failures for that variant. For each variant, we sample from their respective distributions to get a conversion rate. We perform 100,000 simulation runs in our calculations.
The probability of a variant being the best is given by:

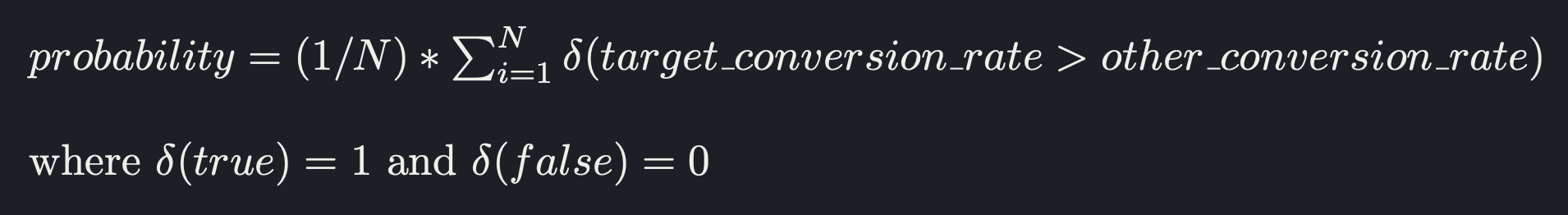
2. Statistical significance
To calculate significance, we measure the expected loss, as described in VWO's SmartStats whitepaper.
To do this, we run a Monte Carlo simulation and calculate the loss as:
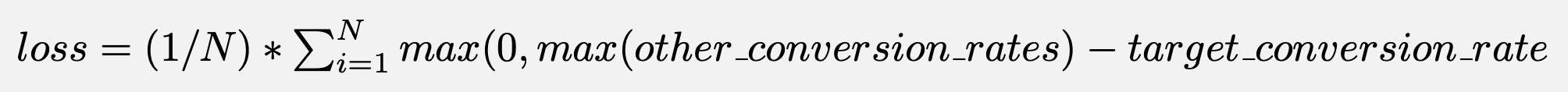

This represents the expected loss in conversion rate if you choose any other variant. If this loss is below 1%, we declare the results significant.
Trend experiment calculations
Trend experiments capture count data. For example, if you want to measure the change in the total count of clicks, you would use this type of experiment.
1. Probability of being the best
We use Monte Carlo simulations to determine the probability of each variant being the best.
Each variant can be modeled as a gamma distribution, with the shape parameter equal to the trend count and the exposure parameter equal to the relative exposure for that variant. For each variant, we sample from their respective distributions to get a count value. We perform 100,000 simulation runs in our calculations.
The probability of a variant being the best is given by:
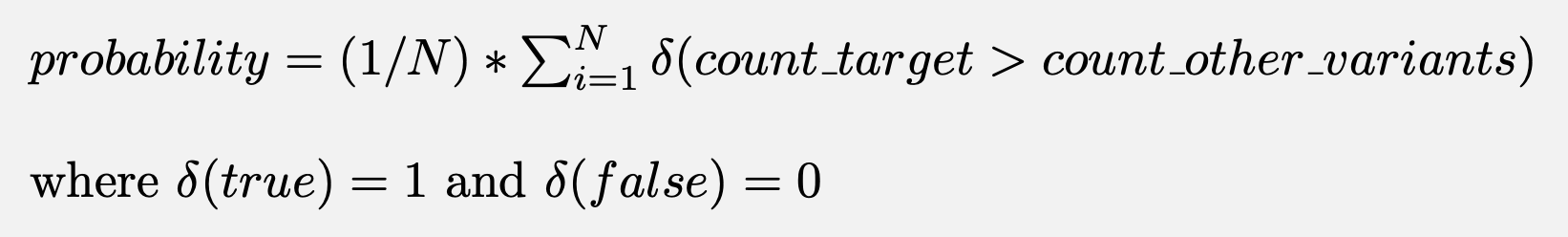
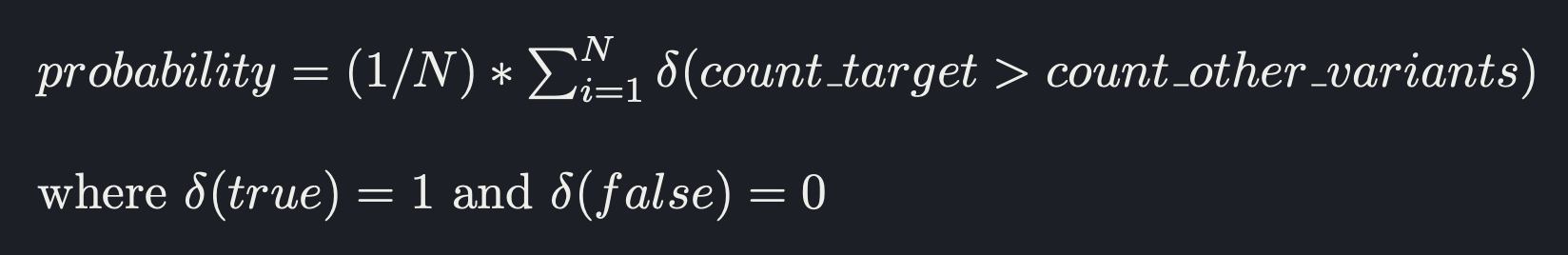
Trend experiment exposure
Trend experiments compare counts of events. Since count data can refer to the total count of events or the number of unique users, we use a proxy metric to measure exposure. The number of times the
feature_flag_calledevent returns control or test is used as the respective exposure for the variant. This event is sent automatically when you callposthog.getFeatureFlag().Note that a variant showing fewer count data can still have a higher probability of being the best if its exposure is much smaller. This is because the relative exposure is taken into account when calculating probabilities.
2. Statistical significance
To calculate significance, we measure p-values using a Poisson means test. Results are significant when the p-value is less than 0.05
How does PostHog determine final significance?
For your results and conclusions to be valid, any experiment must have significant exposures. For instance, if you test a product change and only a handful of users see the change, you can't be sure of its impact. Thus, in the early days of an experiment, data can vary wildly.
Even with a large sample size (e.g. ~10,000 participants), results can be ambiguous. For example, if the difference in conversion rates between variants is less than 1%, it becomes difficult to determine if one variant is truly better than the other. To achieve statistical significance, there must be a sufficient difference between the conversion rates given the exposure size.
Therefore, we have additional criteria to determine what we call final significance. You'll see the green significance banner in PostHog only when all three of the following conditions are met:
- Each variant has more than 100 unique users.
- The statistical significance calculations confirm significance.
- The combined probability of all test variants being the best is greater than 90%.